what is the Mass of an Electron?
The Mass of an Electron is a fundamental subatomic particle that carries a negative electric charge. Together with protons and neutrons, electrons make up the building blocks of atoms. The mass of an electron plays a critical role across scientific disciplines including chemistry, physics, and electronics.
Knowing the mass of the electron enables calculations of atomic and molecular masses, bond energies, and reaction rates in chemistry. In physics, the electron mass determines the scale of quantum effects and influences the behavior of electrons in electric and magnetic fields. Electron mass is a fundamental constant measured to high precision for applications from theoretical physics to engineering.
This article will provide an overview of the electron mass. We will explore the history of measuring the electron mass, its modern accepted value, and its significance across chemistry, electricity, magnetism, and particle physics. Understanding the mass of the electron provides insight into the quantum world and the fundamental structure of matter.
History of Measuring Electron Mass
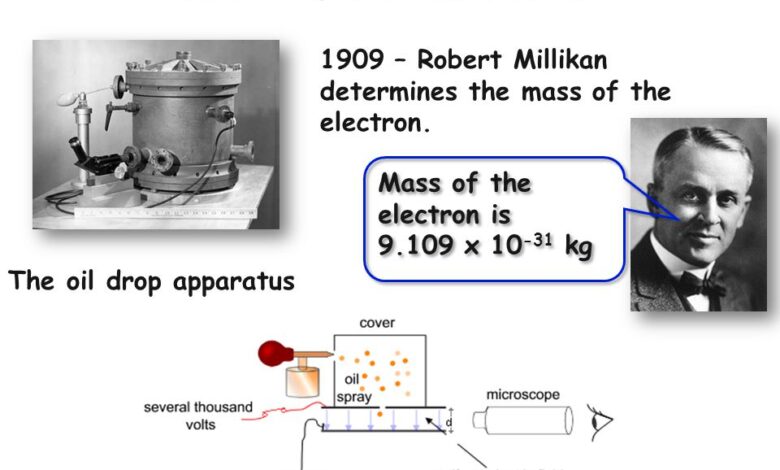
The electron was first discovered in 1897 by J.J. Thomson during investigations into cathode rays. However, it took several more decades before scientists were able to determine the mass of the electron with any precision.
In the early 20th century, physicists relied on indirect methods to estimate the mass of the electron. One approach was to measure x-ray wavelengths from metals. Based on some assumptions about the electron’s charge, these measurements yielded mass values on the order of 10^(-27) kilograms. However, the results were very approximate.
A major breakthrough came with the oil drop experiment performed by Robert Millikan and Harvey Fletcher in 1910-1911. Their setup involved spraying a mist of oil droplets into a chamber with an electric field. By measuring the rate at which the droplets fell under gravity versus their rate of rise when the electric field was applied, Millikan and Fletcher were able to determine the charge on individual droplets. Knowing the charge allowed them to calculate the mass using the balance between gravitational and electric forces.
After tweaking their methods over several years, Millikan published the first accurate measurement of the electron’s mass in 1913. His value of 9.1 x 10^(-28) grams proved remarkably close to today’s accepted value. The oil drop experiment put an end to the wide-ranging estimates and firmly established the mass of the electron for future physicists.
Modern Value for Electron Mass
The currently accepted value for the mass of an electron is 9.10938356 × 10^-31 kilograms. This extremely small number is a fundamental physical constant that physicists have been trying to measure precisely for over a century using different experimental techniques.
The most accurate method used today involves observing the cyclotron motion of an electron in a Penning trap. By applying a magnetic field and an electric field to the trap, scientists can cause the electron to move in a circular path at a characteristic frequency that depends on the charge-to-mass ratio. Since the electron charge is known to high precision, the mass can be calculated based on the measured frequency.
Other approaches used historically include comparing the curvatures of electron and proton trajectories in a magnetic field and measuring the wavelengths of radiation emitted when electrons jump between quantum energy levels in an atom. Each new innovation in measurement science has enabled more precise values for electron mass to be determined over time. The level of precision has increased from 5 significant digits in the 1910s to 11 significant digits in the current accepted value today.
Researchers are continually working to improve the accuracy even further since the electron mass is a fundamental constant used across many areas of physics and chemistry. More precise values allow scientists to test the limits of the standard model of particle physics as well as make more accurate predictions in quantum electrodynamics calculations.
Relation to Atomic Mass Unit
The atomic mass unit (amu) is a standard unit of mass defined based on the mass of a carbon-12 atom. Originally, amu referred to 1/12th the mass of a carbon-12 atom. However, the modern definition is that 1 amu is exactly 1/12 the mass of a free carbon-12 atom at rest.
The amu is approximately equal to the mass of a proton or neutron. However, the amu is defined based on the carbon-12 atom rather than the mass of subatomic particles for greater accuracy and precision.
There is a direct relationship between the mass of an electron and the atomic mass unit. The mass of an electron is approximately 0.0005485799090 amu. In other words, the mass of an electron is roughly 1/1836 of the mass of a proton or neutron. This illustrates the minuscule mass of the electron compared to other subatomic particles.
The small mass of the electron relative to the amu is significant for understanding atomic structure, chemical bonding, and physical properties. The low mass means electrons contribute very little to the total mass of an atom, which is dominated by protons and neutrons. This is why atomic mass correlates closely with the number of protons and neutrons rather than the number of electrons. The mass ratio between electrons and nucleons is a fundamental parameter in physics and chemistry.
Effects on Chemical Properties
The mass of the electron plays an important role in the chemical properties and reactivity of atoms and molecules. A key factor is how the mass of the electron relates to the mass of the atomic nucleus. The nucleus contains protons and neutrons and makes up over 99% of an atom’s mass. Electrons orbit the nucleus and their mass is generally insignificant compared to the nuclear mass.
However, the electron mass still has noticeable effects on periodic trends in the elements. For example, electron mass contributes to effective nuclear charge – the net positive charge experienced by electrons in an atom. As you move left to right across the periodic table, effective nuclear charge increases. This pulls electrons closer to the nucleus, making them higher in energy and less available for chemical reactions. Therefore, electron mass relates to reactivity decreasing as you move from left to right.
The electron mass also connects to atomic radius trends. A larger atomic radius means the electrons are farther from the nucleus. As effective nuclear charge increases left to right, the electron cloud contracts and the radius gets smaller. Heavier electron mass would make this contraction effect more significant.
In summary, the mass of electrons may be small but it has measurable effects on periodic trends. It contributes to how nuclear charge changes and alters atomic sizes. Through these mechanisms, electron mass fundamentally influences the chemical properties of the elements. A heavier or lighter electron would change the energies, sizes and reactivities of atoms in the periodic table.
Role in Electricity and Magnetism
The mass of the electron plays an important role in electricity and magnetism. The electron has an intrinsic electric charge that interacts with electric and magnetic fields. Electron motion in conductors forms electric currents, while organized electron motion produces magnetism.
The electron’s small mass allows it to be easily accelerated by electric forces. This enables electric currents and high electron velocities in conductors. The electron’s charge-to-mass ratio is a key parameter in equations for electron motion under electric and magnetic fields.
The electron’s charge and mass both contribute to its magnetic moment. This magnetic moment allows the intrinsic spin of electrons to produce magnetic effects. The orientation of electron spins leads to ferromagnetism in materials.
The electron’s mass and charge are also key factors in electromagnetic radiation. Oscillating electrons emit electromagnetic waves based on the electron’s acceleration. This leads to important phenomena such as cyclotron radiation and synchrotron radiation. The electron mass controls the wavelength of electromagnetic radiation emitted.
Overall, the electron’s low mass and electric charge enable many essential electromagnetic interactions and effects. From small-scale quantum behaviors to large-scale electric power systems, the electron’s intrinsic properties underpin the workings of electromagnetism across all scales. Further research on electron mass and charge will lead to deeper insights into harnessing electromagnetic phenomena.
In Quantum Physics
The mass of the electron plays an important role in quantum physics and quantum mechanics. Electrons have an intrinsic angular momentum or spin, that is quantized. This means the electron can only have specific discrete values for its spin angular momentum. The magnitude of the electron’s spin angular momentum is related to its mass via the reduced Planck constant.
The electron mass is also critical in the Heisenberg uncertainty principle. This principle states that the position and momentum of a particle cannot be simultaneously measured with arbitrary precision. The more precisely you measure the position, the less precisely you can know the momentum, and vice versa. The mathematical relationship contains the electron mass, Planck’s constant, and the uncertainties in position and momentum.
In addition, the electron mass appears in the de Broglie wavelength equation. This relates the wavelength of matter waves to the mass and momentum of a particle. Electrons can exhibit wave-particle duality, meaning they have both particle and wave properties. The de Broglie wavelength determines the scale over which quantum effects are important for electrons.
Quantum electrodynamics, the quantum field theory of electromagnetism, also depends on the electron mass in its mathematical framework. The mass sets the energy scale for electromagnetic interactions between electrons, photons, and other particles. Precision measurements of the electron mass have provided important tests for validating quantum electrodynamics.
The electron mass is a fundamental parameter that arises throughout quantum physics. Along with Planck’s constant and the speed of light, the electron mass characterizes many quantum phenomena and relationships. Its precise value is essential for making accurate predictions in quantum mechanics and quantum field theories.
Relativistic Effects
According to Einstein’s theory of special relativity, objects with mass increase in relativistic mass as they approach the speed of light. This means electrons traveling at very high velocities will have greater mass than when at rest.
The relativistic mass m of an electron can be calculated as:
m = m0 / √(1 – v2/c2)
Where m0 is the rest mass, v is the velocity, and c is the speed of light. This equation shows that as the velocity v approaches c, the denominator approaches zero, leading to an unbounded increase in the relativistic mass m.
Experiments have confirmed this relativistic mass increase at particle accelerators. As electrons are accelerated to velocities close to the speed of light, their observed mass deviates more and more from the rest mass. This is one of the observed phenomena that provides evidence for Einstein’s theory.
The relativistic increase has important effects for high-energy electrons in applications like particle physics research, accelerator physics, and astrophysics studies. Heavier electrons at high speeds carry more momentum and energy, influencing their interactions and behaviors. Accounting for relativistic effects is crucial for proper analysis and predictions.
New physics may emerge at ultra-relativistic speeds close to the speed of light. As electrons approach the limit of c, their properties are stretched to extremes predicted by relativity. This offers opportunities to discover new quantum effects and test the robustness of physical theories at their boundaries. More research is needed to fully explore the relativistic realm for electrons and other fundamental particles.
Significance in Particle Physics
The electron is considered one of the fundamental particles that make up all matter. It is classified as an elementary particle or a fermion in the Standard Model of particle physics. This model describes the basic building blocks of the universe and how they interact through fundamental forces.
As an elementary particle, the electron cannot be broken down into smaller constituents. It has no known internal structure and is considered a point particle with no dimensions. The electron is one of a class of particles called leptons, which interact through the weak force, electromagnetic force, and gravity.
The electron plays a key role in theories describing three of the four fundamental forces – electromagnetism, the weak force, and the strong force. Its interactions with other particles, such as protons, neutrons, and neutrinos, shape the structure and stability of atoms. The electron’s antiparticle is called the positron. When an electron collides with a positron, they annihilate each other and produce energy in the form of gamma ray photons.
The properties of the electron, including its mass, charge, and spin, are critical parameters in the Standard Model. Precision measurements of the electron mass help test the validity of the model. Any deviations from theoretical predictions would suggest new physics beyond the Standard Model. Experiments are also searching for heavier versions of the electron that may exist at higher energy scales. Discovering new elementary particles would expand our understanding of matter’s most fundamental building blocks.
Open Questions and Future Research
The most precise measurements of the electron mass have uncertainties on the order of 1 part per billion. While this is remarkably precise, there are still open questions about whether the electron mass is truly constant or could vary under certain conditions. Some theories in physics predict that fundamental constants like the electron mass could change over time or could have different values under extreme conditions like near black holes.
One major open area is trying to measure the electron mass with even greater precision. Using advanced techniques like Penning traps, there are efforts underway to improve measurements by an order of magnitude or more. Any small deviations from the accepted value could indicate new physics such as extra dimensions predicted by string theory.
Researchers are also studying whether the inertial and gravitational mass of the electron are identical. Einstein’s equivalence principle predicts they should be equal, but extremely high precision measurements could potentially detect tiny differences that would challenge existing theories.
There are also efforts to measure the electron’s mass at very high energies, such as in particle colliders. Most measurements are done with electrons at rest, but what happens when electrons are accelerated close to the speed of light? Some hypotheses predict relativistic effects could subtly alter the electron’s observed mass at very high velocities.
The electron mass plays a central role in the standard model of particle physics and our understanding of the basic laws of the universe. While it seems well-determined, pushing the precision further using next-generation techniques could lead to transformative discoveries about the nature of reality. The electron mass therefore remains an area of intense focus, speculation, and open questions on the cutting edge of physics. Even the most precisely measured quantities can still harbor plenty of mysteries when examined closely enough.





